坐标系

笛卡尔坐标系（法语：système de coordonnées cartésiennes，英语：Cartesian coordinate system，也称直角坐标系）在数学中是一种正交坐标系，由法国数学家勒内·笛卡尔引入而得名。二维的直角坐标系是由两条相互垂直、相交于原点的数线构成的。
在平面内，任何一点的坐标是根据数轴上对应的点的坐标设定的。在平面内，任何一点与坐标的对应关系，类似于数轴上点与坐标的对应关系。

采用笛卡尔坐标系，几何形状可以用代数公式明确地表达出来。几何形状的每一个点的直角坐标必须遵守这个代数公式。

直线: ${\displaystyle ax+by+c=0}$
斜截式 : ${\displaystyle y=mx+k}$
圆 : ${\displaystyle (x-a)^{2}+(y-b)^{2}=r^{2}}$

众所周知，OpenGL使用的是右手坐标系，而Direct3D使用的是左手坐标系。

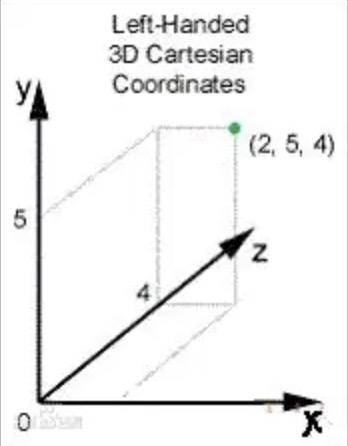
Unity 使用的是左手坐标系。

点和向量

点是三维空间中的某个坐标，是绝对的，它的值是参照原点的，而向量用于表示力和速度等具有方向和大小的量，通常用具有长度和方向的线段来表示，虽然他们都具有三个分量，但对于向量，如果将向量放在坐标系中的任何位置（平移），都不会改变其性质，因为向量表示的是方向和大小，与位置距离无关，它的值是相对与基准点的。

向量的模

向量的绝对值就是向量的长度，也称模，计算公式为：

$l =\sqrt{a^2+b^2+c^2} $

单位向量

单位向量就是模(向量长度)为1的向量，也就是某向量每单位长度的向量。单位向量u的计算公式为：

$u=\frac{V}{\left | V \right | } $

向量的运算

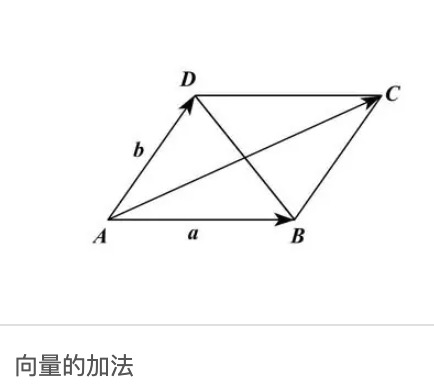
向量的加法

向量的加法得到的是一个向量

加法公式：

$u+v=w=(u_{x}+v_{x}, u_{y}+v_{y})$

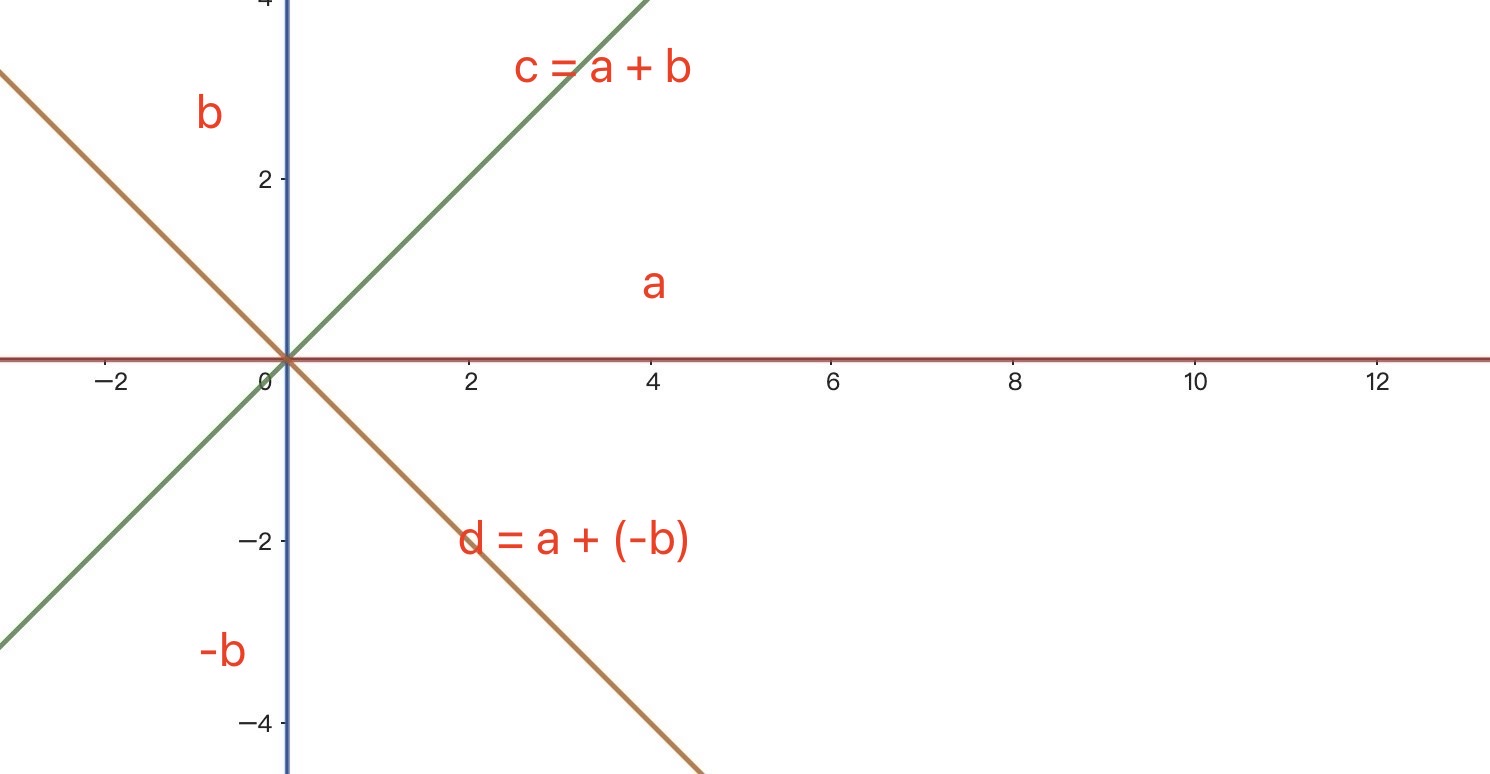
向量的减法

向量的减法得到的也还是一个向量

减法公式：

$u-v=w=(u_{x}-v_{x}, u_{y}-v_{y})$

向量的点乘

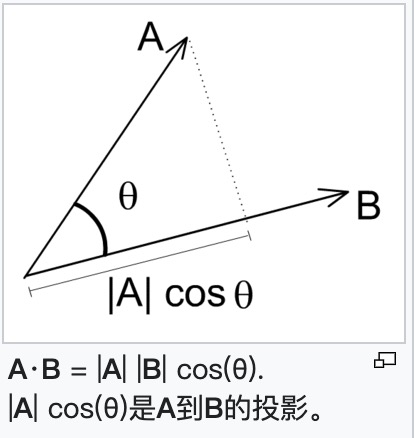
向量的点乘代表的是一个投影，公式如下：

$\vec{a} * \vec{b} = \left | \vec{a} \right | * \left | \vec{b} \right | * \cos \theta $

其中 $\theta$ 是向量 $\vec{a}$ 和向量 $\vec{b}$ 的夹角

举一个最简单的例子，如果 $\theta$ 等于 45°，那么斜边投影在侧边上的长度刚好为1。

向量的叉乘

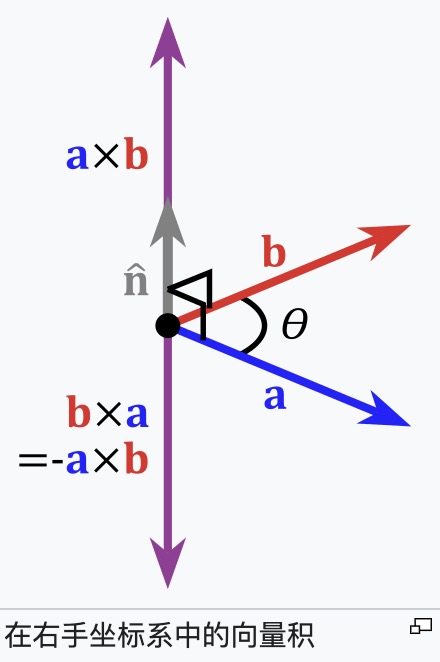
Cross

这是一个三维坐标系，其中向量 $\vec{w}$ 向量 $\vec{v}$ 向量 $\vec{u}$ 分别代表每个轴，如果这个时候：

$\vec{w}$ = $\vec{u}$ x $\vec{v}$

$\vec{w}$ 的指向按右手定则从 $\vec{u}$ 转向 $\vec{v}$ 来确定

$\vec{w}$ 向量的模长在数值上等于以 $\vec{u}$、$\vec{v}$ 形成的夹角 $\theta$ 组成的平行四边形的面积

矩阵（Matrix）

在数学中，矩阵（Matrix）是一个按照长方阵列排列的复数或实数集合，最早来自于方程组的系数及常数所构成的方阵。

由 m × n 个数aij排成的m行n列的数表称为m行n列的矩阵，简称m × n矩阵。记作：

这 m×n 个数称为矩阵A的元素，简称为元，数aij位于矩阵A的第i行第j列，称为矩阵A的(i,j)元，以数 aij为(i,j)元的矩阵可记为(aij)或(aij)m × n，m×n矩阵A也记作Amn。
元素是实数的矩阵称为实矩阵，元素是复数的矩阵称为复矩阵。而行数与列数都等于n的矩阵称为n阶矩阵或n阶方阵。